Actividades

Introducción Conceptual: Actividad es un concepto que procede del vocablo latino activĭtas. Este término es fruto de la suma de tres componentes claramente diferenciados como son los siguientes:

• "Actus”, que puede traducirse como “llevado a cabo”.
• "-ivo”, que se utiliza para indicar relación activa o pasiva.
• El sufijo “-dad”, que se emplea para indicar “calidad”

Se trata de las acciones que desarrolla un individuo o una institución de manera cotidiana, como parte de sus obligaciones, tareas o funciones.

Dentro de la Cátedra Seminario II, se efectuó el desarrollo de actividades según las habilidades y capacidades que se desean acrecentar,  en base al modelo Tpack y teniendo en cuenta el tema trabajado hasta el momento, en mi caso "Continuidad de Funciones". Además se describió anteriormente, las decisiones curriculares, pedagógicas y tecnológicas que como docentes  se tomamos, al momento de planificar dichas actividades.
Para diseñar las actividades se debe tener en cuenta el momento de la clase en el que nos ubicamos. Es por ello que, según la fase de la secuencia didáctica a diseñar las actividades se clasifican en:

a)Actividades Iniciales o Globales: los estudiantes abordan situaciones en las que pueden comprender el problema significativo del contexto y el desafío que le propone el docente. Aquí pueden diseñar un plan para resolver el desafío, y de esa manera, contribuir creativamente a la resolución de problemáticas del entorno. Además, es necesario que los estudiantes conozcan los criterios de evaluación que se tendrán en cuenta, sea por medio de rúbricas o listas de cotejo.

b) Actividades de Desarrollo o Analíticas: en esta fase el docente crea espacios y destina tiempos para que los estudiantes se apropien de saberes necesarios para enriquecer el plan de resolución del desafío, como también las instancias donde los estudiantes puedan implementar el plan elaborado. Implica instancias de evaluaciones de procesos, como por ejemplo los trabajos prácticos o evaluaciones escritas, que permitan verificar la comprensión y apropiación significativa de nociones o procedimientos. Es conveniente que las mismas incluyan diversas situaciones que favorezcan un análisis integral asociado a las capacidades, en vez de mera resolución mecánica de ejercicios que apele exclusivamente a la memoria.

c) Actividades de Cierre o Comunicación: en esta fase se ofrecen espacios y tiempos para la metacognición. Los estudiantes comunican el plan implementado, sus resultados, sus dificultades y los aprendizajes construidos mediante la experiencia. Ayudados con las rúbricas de evaluación y/o la lista de cotejo pueden ir evaluando sus logros, sus avances en los aprendizajes, en relación con las capacidades. 

Además se tuvo en cuenta la clasificación propuesta según los estándares del National Council of Teachers of Mathematics (NCTM), y revisar la gama de
actividades de aprendizaje, que promuevan la integración efectiva de tecnología, pedagogía y contenido, las cuales son: Actividades para Considerar, para Practicar, para Interpretar, para Producir, para Aplicar, para Evaluar y para Crear.

A continuación se muestran las actividades que han sido diseñadas en las distintas herramientas educativas asociadas al tema "Continuidad de Funciones" ,que es el contenido matemático sobre el que se ha trabajado y el que ha sido corregido por las docentes a cargo de la cátedra:

Actividad de Inicio:

La consigna que se desarrollará a continuación se encuentra dentro las Actividades para Considerar ya que los alumnos deberán comprender la situación problemática planteada y posteriormente intercambiar con sus compañeros opiniones e ideas.

Se trabajará de manera individual si cada alumno cuenta con computadora o teléfono y sobre todo con internet para descargar Geogebra. En caso contrario, se realizarán grupos de acuerdos a la conectividad y disponibilidad de equipos portátiles. Deberán realizar la consigna en sus cuadernos y al finalizar se hará una puesta en común sobre lo trabajado. Esto permitirá que los alumnos vayan familiarizándose con el contenido que se pretende enseñar e ir analizando de a poco distintas características del mismo.

Consigna: Juan y su familia el fin de semana decidieron emprender un viaje, pero mientras circulaban por la ruta 246 que se dirige a Caucete, se encontraron con que en el medio de ella había un pozo que les impedía seguir su camino.

·   ¿Qué punto de esa trayectoria tuvieron que arreglar para que puedan continuar su viaje con normalidad?

·    ¿Podrías decir de qué tipo de función estamos hablando?

·     Anima en Geogebra el punto F, de acuerdo a eso y teniendo en cuenta la fórmula de la función, analiza e indica cuál sería el dominio de dicha función. ¿Presenta alguna restricción?

Actividades de Desarrollo:

La siguiente consigna forma parte tanto de las Actividades para Practicar en donde se realizarán cálculos, comparaciones entre los mismos, como dentro de las Actividades para Interpretar las representaciones.

Al igual que la actividad anterior, se llevará a cabo de manera individual al menos que no se cuente con equipos portátiles y conectividad suficiente.

Cada archivo de Geogebra representa una situación distinta y para realizar los cálculos que se solicitan deben escribir en la barra de entrada h(x) (no siempre será h, eso depende del nombre que presente la función) y para lo demás, Limite, LimiteIzquierda, LimiteDerecha y deberán completar con la función y el valor en el que se desea calcular esos límites.

Las preguntas planteadas en tanto en la consigna 1 como en la 2 deberán estar respuestas en los cuadernos de los alumnos, pues servirán para poder dar posteriormente el concepto de continuidad de funciones.

En cuanto a la consigna número 3, también debe estar presente en el cuaderno la resolución de la misma.

Una vez que todos hayan terminado de realizar la consigna se intercambiarán ideas y opiniones entre todos. 

Consigna 1:

Matías y sus amigos todas las tardes salen a divertirse y andar en skaters en las rampas de la plaza de su barrio.

Para practicar Matías decide probar tres rampas diferentes.

Realiza los siguientes pasos para cada una de las rampas:

·         Anima a Mati en su patineta para visualizar la función que recorre

·         Luego calcula en la barra de entrada el límite de la función, límite a izquierda, límite a derecha y la imagen para 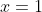 para la primera rampa, 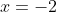  para la segunda rampa y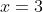 para la tercera rampa

Para calcularlos deberás escribir en la barra de entrada h(x) (no siempre será h, eso depende del nombre que presente la función) y para lo demás, Limite, LimiteIzquierda, LimiteDerecha y deberán completar con la función y el valor en el que se desea calcular esos límites.

·         Inserta estos datos en un cuadro de texto dinámico seleccionando en la barra de herramientas de Geogebra la opción “Deslizador” y dentro de ella “Texto”

                            

El contenido que deberá presentar el texto será parecido a lo siguiente:

                                

·         Mueve los deslizadores y observa cómo cambia lo calculado anteriormente

De acuerdo a lo realizado en Geogebra, responde las preguntas que se muestran a continuación:

ü  ¿Qué diferencias observa en las distintas gráficas?

ü  ¿Qué pasa con los límites a izquierda y a derecha?

ü  ¿La imagen en cada uno de los x indicados más arriba coincide con el límite de la función?

Situación 1:


Situación 2 Situación 3Consigna 2:
 Mueve los deslizadores y analiza para que valores a y b las funciones p(x),q(x) y r(x) no presentan saltos o bien para que su trazo sea continuo. Sugerencia: Para calcular los valores a y b que hacen que p(x) no presentan saltos o bien para que su trazo sea continuo, oculta en Geogebra q(x) y r(x); y así sucesivamente con las demás funciones. 

Actividades de Cierre:
Se retomará lo trabajado en las actividades de desarrollo y de acuerdo a eso se institucionará el concepto de "Continuidad de Funciones" otrogándoles a los alumnos el documento que se muestra a continuación en donde podrán visualizar cuando una función es contínua:

Institucionalización by Micaela Rodriguez on Scribd